Binning

Binning is a technique used to group continuous values into a smaller number of bins. This is particularly useful when you have irregularly distributed data and want to analyze it on a regular grid. In this example, we will use pyinterp’s 2D binning functionality to calculate drifter velocity statistics in the Black Sea over a 9-year period.

import cartopy.crs
import matplotlib.pyplot
import numpy

import pyinterp
import pyinterp.backends.xarray
import pyinterp.tests

Loading the Data

First, we load the drifter data, which includes longitude, latitude, and velocity components (u and v).

ds = pyinterp.tests.load_aoml()

We then calculate the velocity magnitude from the u and v components.

norm = (ds.ud**2 + ds.vd**2)**0.5

Defining the Grid

Next, we define the 2D grid on which we will bin the data. The grid is defined by two axes: one for longitude and one for latitude.

binning = pyinterp.Binning2D(
    pyinterp.Axis(numpy.arange(27, 42, 0.3, dtype=numpy.float64),
                  is_circle=True),
    pyinterp.Axis(numpy.arange(40, 47, 0.3, dtype=numpy.float64)))
print(binning)

<pyinterp.binning.Binning2D>
Axis:
  x: <pyinterp.core.Axis>
  min_value: 27
  max_value: 41.7
  step     : 0.3
  is_circle: false
  y: <pyinterp.core.Axis>
  min_value: 40
  max_value: 46.9
  step     : 0.3
  is_circle: false

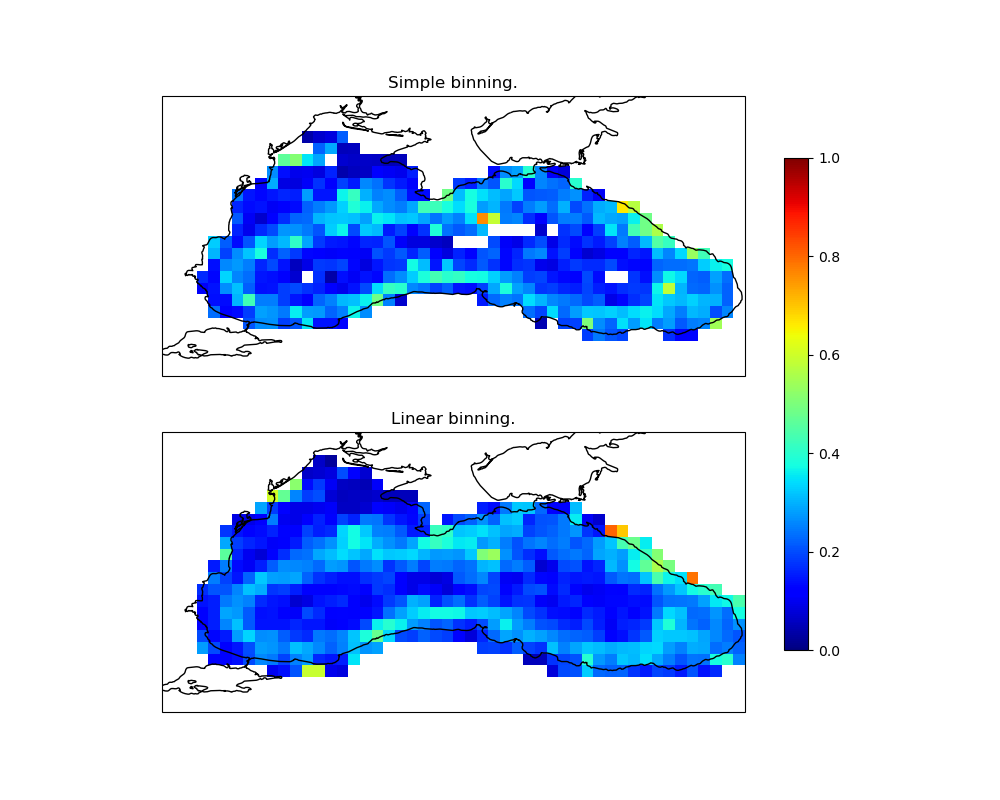
Simple Binning

With simple binning, each data point is assigned to the bin that contains its coordinates. We push the data into the bins and then compute the mean of the values in each bin.

binning.clear()
binning.push(ds.lon, ds.lat, norm, True)
simple_mean = binning.variable('mean')

Note

For datasets larger than the available RAM, you can use Dask for parallel computation. The push_delayed method returns a Dask graph, which can be computed to get the result.

binning = binning.push_delayed(lon, lat, data).compute()

You can also compute other statistical variables like variance, minimum, and maximum using the variable method.

Linear Binning

Linear binning is a more advanced technique where each data point contributes to the four nearest bins, weighted by its distance to the center of each bin. This generally produces a smoother result.

binning.clear()
binning.push(ds.lon, ds.lat, norm, False)
linear_mean = binning.variable('mean')

Visualizing the Results

Finally, we visualize the results of both simple and linear binning.

fig = matplotlib.pyplot.figure(figsize=(10, 8))
fig.subplots_adjust(left=0.05, right=0.95, top=0.95, bottom=0.05, hspace=0.25)
ax1 = fig.add_subplot(211, projection=cartopy.crs.PlateCarree())
lon, lat = numpy.meshgrid(binning.x, binning.y, indexing='ij')
pcm = ax1.pcolormesh(lon,
                     lat,
                     simple_mean,
                     cmap='jet',
                     shading='auto',
                     vmin=0,
                     vmax=1,
                     transform=cartopy.crs.PlateCarree())
ax1.set_extent([27, 42, 40, 47], crs=cartopy.crs.PlateCarree())
ax1.coastlines()
ax1.set_title('Simple Binning')

ax2 = fig.add_subplot(212, projection=cartopy.crs.PlateCarree())
pcm = ax2.pcolormesh(lon,
                     lat,
                     linear_mean,
                     cmap='jet',
                     shading='auto',
                     vmin=0,
                     vmax=1,
                     transform=cartopy.crs.PlateCarree())
ax2.set_extent([27, 42, 40, 47], crs=cartopy.crs.PlateCarree())
ax2.coastlines()
ax2.set_title('Linear Binning')
fig.colorbar(pcm, ax=[ax1, ax2], shrink=0.8)

<matplotlib.colorbar.Colorbar object at 0x12aad3c20>

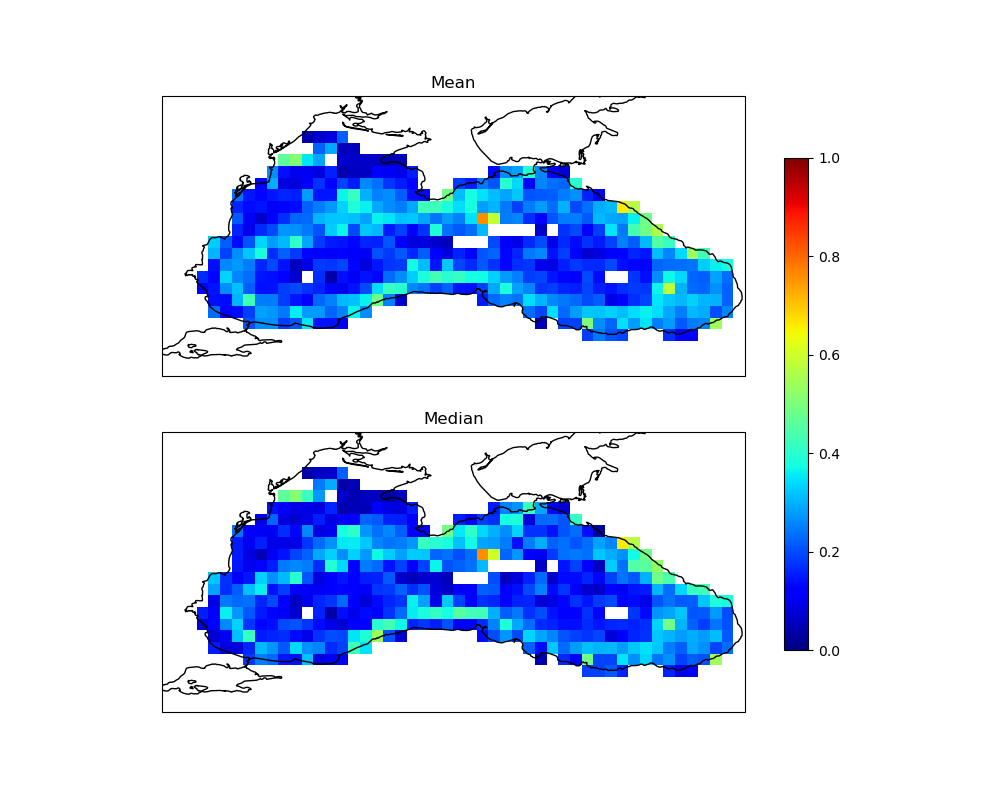
Histogram2D

The Histogram2D class is similar to the Binning2D class, but it calculates the histogram of the data in each bin instead of the statistics.

Let’s calculate the 2D histogram of the drifter data.

hist = pyinterp.Histogram2D(
    pyinterp.Axis(numpy.arange(27, 42, 0.3, dtype=numpy.float64),
                  is_circle=True),
    pyinterp.Axis(numpy.arange(40, 47, 0.3, dtype=numpy.float64)))
hist.push(ds.lon, ds.lat, norm)

We can then visualize the histogram.

fig = matplotlib.pyplot.figure(figsize=(10, 4))
fig.subplots_adjust(left=0.05, right=0.95, top=0.95, bottom=0.05, hspace=0.25)
ax1 = fig.add_subplot(111, projection=cartopy.crs.PlateCarree())
pcm = ax1.pcolormesh(lon,
                     lat,
                     hist.variable(),
                     cmap='jet',
                     shading='auto',
                     transform=cartopy.crs.PlateCarree())
ax1.set_extent([27, 42, 40, 47], crs=cartopy.crs.PlateCarree())
ax1.coastlines()
ax1.set_title('2D Histogram')
fig.colorbar(pcm, ax=ax1, shrink=0.8)

<matplotlib.colorbar.Colorbar object at 0x12ae7b140>