2D Interpolation

This example illustrates how to perform 2D interpolation of a variable on a regular grid. The pyinterp library provides several interpolation methods, and this guide will walk you through bivariate and bicubic interpolation.

import cartopy.crs
import matplotlib
import matplotlib.pyplot
import numpy

import pyinterp
import pyinterp.backends.xarray
import pyinterp.tests

Bivariate Interpolation

Bivariate interpolation is a common method for estimating the value of a variable at a new point based on its surrounding grid points. In this section, we will perform bivariate interpolation using pyinterp.

First, we load the data and create the interpolator object. The constructor will automatically detect the longitude and latitude axes. If it fails, you can specify them by setting the units attribute to degrees_east and degrees_north. If your grid is not geodetic, set the geodetic parameter to False.

ds = pyinterp.tests.load_grid2d()
interpolator = pyinterp.backends.xarray.Grid2D(ds.mss)

Next, we define the coordinates where we want to interpolate the grid. To avoid interpolating at the grid points themselves, we shift the coordinates slightly.

mx, my = numpy.meshgrid(
    numpy.arange(-180, 180, 1) + 1 / 3.0,
    numpy.arange(-89, 89, 1) + 1 / 3.0,
    indexing="ij",
)

Now, we interpolate the grid to the new coordinates using the bivariate method.

mss = interpolator.bivariate(
    coords={"lon": mx.ravel(), "lat": my.ravel()}
).reshape(mx.shape)

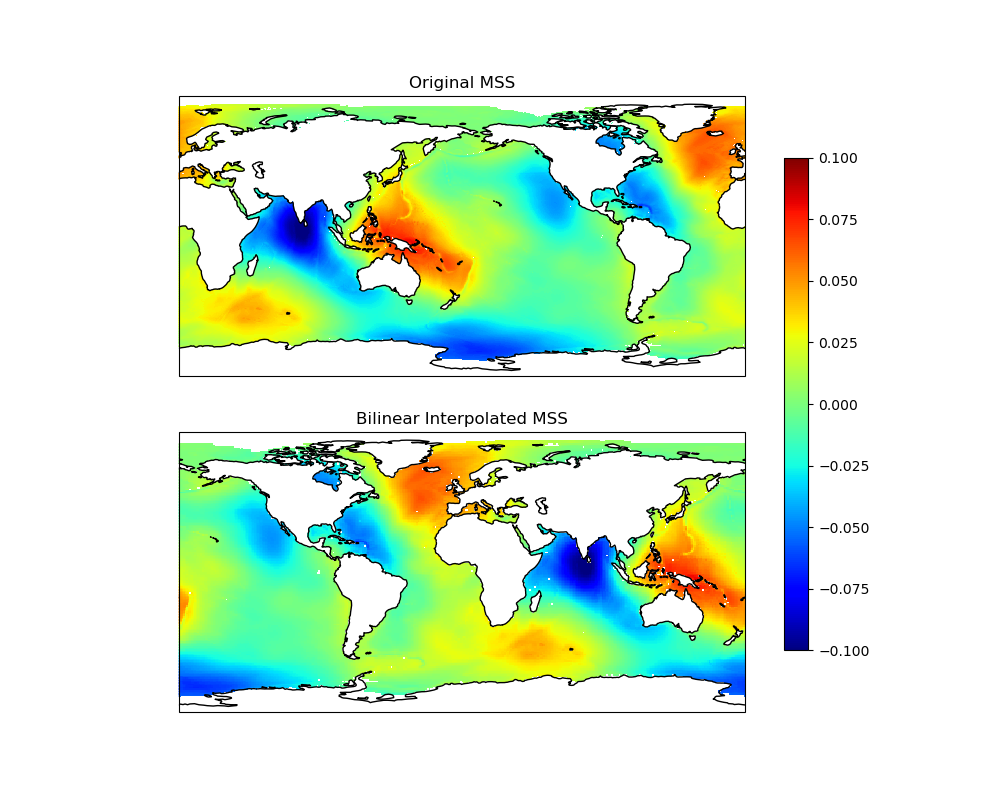
To visualize the results, we can plot the original grid and the interpolated grid.

fig = matplotlib.pyplot.figure(figsize=(10, 8))
fig.subplots_adjust(left=0.05, right=0.95, top=0.95, bottom=0.05, hspace=0.25)
ax1 = fig.add_subplot(
    211, projection=cartopy.crs.PlateCarree(central_longitude=180)
)
lons, lats = numpy.meshgrid(ds.lon, ds.lat, indexing="ij")
pcm = ax1.pcolormesh(
    lons,
    lats,
    ds.mss.T,
    cmap="jet",
    shading="auto",
    transform=cartopy.crs.PlateCarree(),
    vmin=-0.1,
    vmax=0.1,
)
ax1.set_extent([-180, 180, -90, 90], crs=cartopy.crs.PlateCarree())
ax1.coastlines()
ax1.set_title("Original MSS")
ax2 = fig.add_subplot(212, projection=cartopy.crs.PlateCarree())
pcm = ax2.pcolormesh(
    mx,
    my,
    mss,
    cmap="jet",
    shading="auto",
    transform=cartopy.crs.PlateCarree(),
    vmin=-0.1,
    vmax=0.1,
)
ax2.set_extent([-180, 180, -90, 90], crs=cartopy.crs.PlateCarree())
ax2.coastlines()
ax2.set_title("Bilinear Interpolated MSS")
fig.colorbar(pcm, ax=[ax1, ax2], shrink=0.8)

<matplotlib.colorbar.Colorbar object at 0x1350bb230>

The bivariate method supports multiple interpolation techniques:

• Default methods: bilinear, nearest neighbor, inverse distance weighting

• Advanced methods: bicubic, akima, akima_periodic, c_spline, c_spline_not_a_knot, c_spline_periodic, linear, polynomial, steffen

For geodetic grids, distance calculations use the Haversine formula.

Windowed Interpolators

Bicubic and spline interpolation provides smoother results compared to bilinear by using a windowed approach that considers a neighborhood of grid points within a calculation window. You can use it by passing method='bicubic' to the bivariate method or other supported methods.

Warning

When using these interpolators, pay attention to NaN values. If the calculation window contains even a single NaN, the result of the interpolation will also be NaN, due to NaN propagation in arithmetic operations. This means the masked region effectively grows during interpolation. To avoid this behavior, you should pre-process the grid to replace or remove NaN values.

Note

When using windowed interpolation methods like bicubic, the behavior near grid edges is controlled by the boundary_mode parameter. Two modes are available:

• undef: (Undefined Boundary) - Default: The interpolation window must fit entirely within the grid. If a query point is too close to the edge and the full window cannot be extracted, the interpolation returns NaN. This ensures strict interpolation quality but may result in undefined values near boundaries.

• shrink (Shrink Boundary): The interpolation window adaptively shrinks at grid boundaries to use available data. For example, a 4x4 bicubic window near an edge may become 3x4 or 2x4. This allows interpolation closer to edges but may affect smoothness in those regions.

The following code performs bicubic interpolation on the same grid.

mss_bicubic = interpolator.bivariate(
    coords={"lon": mx.ravel(), "lat": my.ravel()}, method="bicubic"
).reshape(mx.shape)

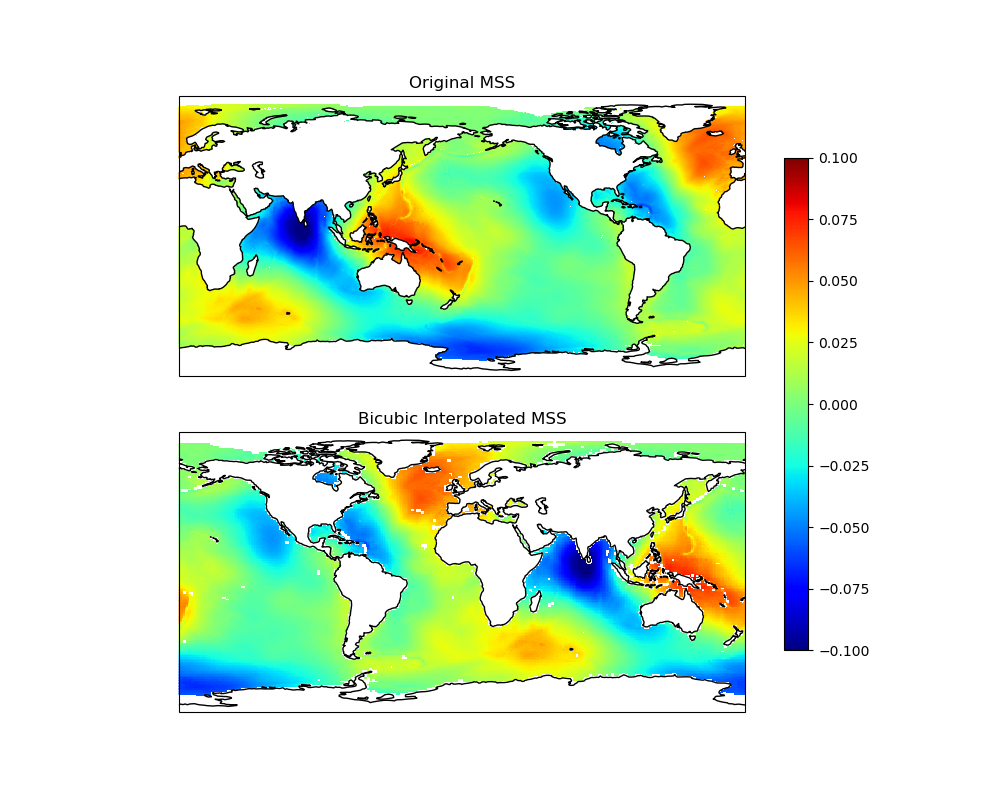
Let’s visualize the result of the bicubic interpolation and compare it with the original data.

fig = matplotlib.pyplot.figure(figsize=(10, 8))
fig.subplots_adjust(left=0.05, right=0.95, top=0.95, bottom=0.05, hspace=0.25)
ax1 = fig.add_subplot(
    211, projection=cartopy.crs.PlateCarree(central_longitude=180)
)
pcm = ax1.pcolormesh(
    lons,
    lats,
    ds.mss.T,
    cmap="jet",
    shading="auto",
    transform=cartopy.crs.PlateCarree(),
    vmin=-0.1,
    vmax=0.1,
)
ax1.set_extent([-180, 180, -90, 90], crs=cartopy.crs.PlateCarree())
ax1.coastlines()
ax1.set_title("Original MSS")
ax2 = fig.add_subplot(212, projection=cartopy.crs.PlateCarree())
pcm = ax2.pcolormesh(
    mx,
    my,
    mss_bicubic,
    cmap="jet",
    shading="auto",
    transform=cartopy.crs.PlateCarree(),
    vmin=-0.1,
    vmax=0.1,
)
ax2.set_extent([-180, 180, -90, 90], crs=cartopy.crs.PlateCarree())
ax2.coastlines()
ax2.set_title("Bicubic Interpolated MSS")
fig.colorbar(pcm, ax=[ax1, ax2], shrink=0.8)

<matplotlib.colorbar.Colorbar object at 0x13410fcb0>

The bivariate method with method='bicubic' accepts additional parameters to control the interpolation window size and boundary handling:

mss = interpolator.bivariate(
    coords={"lon": mx.ravel(), "lat": my.ravel()},
    method="bicubic",
    boundary_mode="shrink",
    half_window_size_x=3,
    half_window_size_y=3,
).reshape(mx.shape)

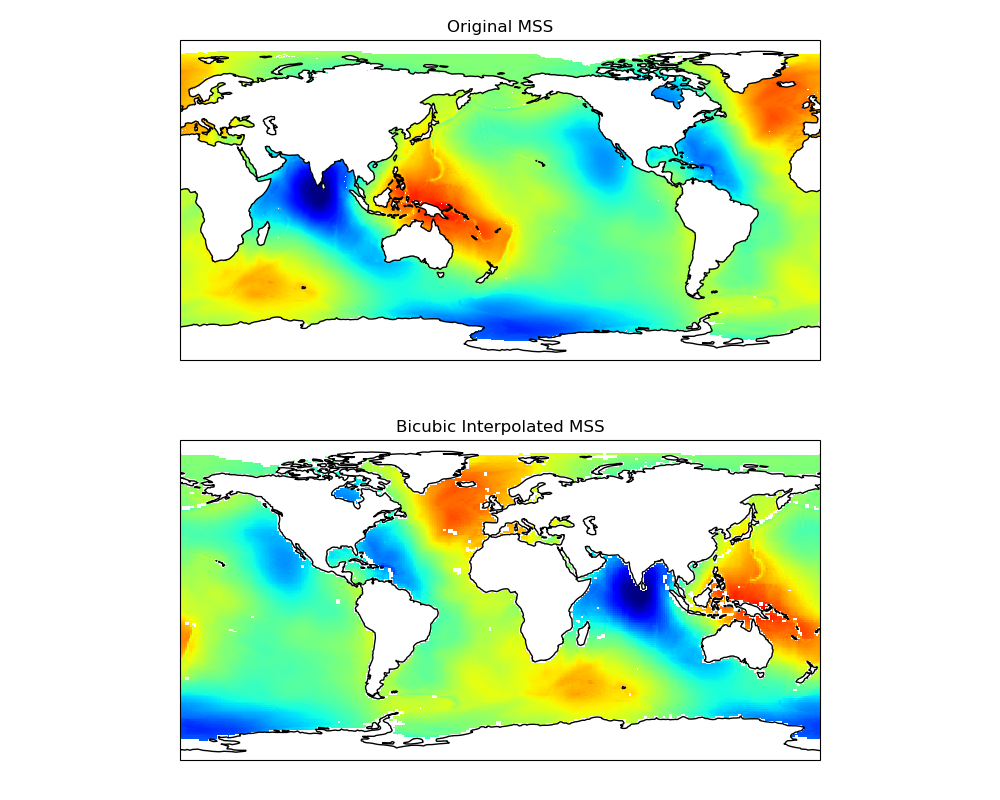
Finally, let’s visualize the bicubic interpolation result with the custom parameters.

fig = matplotlib.pyplot.figure(figsize=(10, 8))
fig.subplots_adjust(left=0.05, right=0.95, top=0.95, bottom=0.05, hspace=0.25)
ax1 = fig.add_subplot(
    211, projection=cartopy.crs.PlateCarree(central_longitude=180)
)
pcm = ax1.pcolormesh(
    lons,
    lats,
    ds.mss.T,
    cmap="jet",
    shading="auto",
    transform=cartopy.crs.PlateCarree(),
    vmin=-0.1,
    vmax=0.1,
)
ax1.set_extent([-180, 180, -90, 90], crs=cartopy.crs.PlateCarree())
ax1.coastlines()
ax1.set_title("Original MSS")
ax2 = fig.add_subplot(212, projection=cartopy.crs.PlateCarree())
pcm = ax2.pcolormesh(
    mx,
    my,
    mss,
    cmap="jet",
    shading="auto",
    transform=cartopy.crs.PlateCarree(),
    vmin=-0.1,
    vmax=0.1,
)
ax2.set_extent([-180, 180, -90, 90], crs=cartopy.crs.PlateCarree())
ax2.coastlines()
ax2.set_title("Bicubic Interpolated MSS")

Text(0.5, 1.0, 'Bicubic Interpolated MSS')