Note
Go to the end to download the full example code. or to run this example in your browser via Binder
Orbit Interpolation¶
This library facilitates the interpolation of orbit ephemerides from a template file that contains satellite positions for a single orbit cycle. It supports the propagation of the orbit over time, making it useful for simulations and other applications that require orbit propagation.
To begin, we will load the orbit ephemerides from the template file. In this example, we will create a simple function to load the data from the test file.
import pathlib
import cartopy.crs as ccrs
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pyinterp
import pyinterp.tests
def load_test_ephemeris(
filename: pathlib.Path
) -> tuple[float, np.ndarray, np.ndarray, np.ndarray, np.timedelta64]:
"""Loads the ephemeris from a text file.
Args:
filename: Name of the file to be loaded.
Returns:
A tuple containing the height of the orbit, the ephemeris and the
duration of the cycle.
"""
with open(filename) as stream:
lines = stream.readlines()
def to_dict(comments) -> dict[str, float]:
"""Returns a dictionary describing the parameters of the orbit."""
result = {}
for item in comments:
assert item.startswith('#'), 'Comments must start with #'
key, value = item[1:].split('=')
result[key.strip()] = float(value)
return result
# The two first lines are the header and contain the height and the
# duration of the cycle in fractional days.
settings = to_dict(lines[:2])
del lines[:2]
# The rest of the lines are the ephemeris
ephemeris = np.loadtxt(lines,
delimiter=' ',
dtype={
'names':
('time', 'longitude', 'latitude', 'height'),
'formats': ('f8', 'f8', 'f8', 'f8')
})
return (
settings['height'],
ephemeris['longitude'],
ephemeris['latitude'],
ephemeris['time'].astype('timedelta64[s]'),
np.timedelta64(int(settings['cycle_duration'] * 86400.0 * 1e9), 'ns'),
)
Set the path to the test file
swot_calval_ephemeris_path = pyinterp.tests.swot_calval_ephemeris_path()
ephemeris = load_test_ephemeris(swot_calval_ephemeris_path)
Compute the orbit properties from the provided ephemeris
orbit = pyinterp.calculate_orbit(*ephemeris)
The orbit object provides a method to calculate the number of passes per cycle
print(orbit.passes_per_cycle())
28
To get the cycle duration, and the orbit duration we can use the cycle_duration method and the orbit_duration method respectively.
print(orbit.cycle_duration().astype('m8[ms]').item())
print(orbit.orbit_duration().astype('m8[ms]').item())
23:25:23.172000
1:40:23.083000
We can also retrieve the pass duration for a given pass number:
print(orbit.pass_duration(2).astype('m8[ms]').item())
0:55:44.350000
A utility function is provided to compute an absolute pass number from a relative pass number and to decode the absolute pass number back into a relative pass number. This function is useful for storing the pass number in a database or indexing the passes in a file, among other applications.
absolute_pass_number = orbit.encode_absolute_pass_number(cycle_number=11,
pass_number=2)
print(absolute_pass_number)
cycle_number, pass_number = orbit.decode_absolute_pass_number(
absolute_pass_number)
print(cycle_number, pass_number)
282
11 2
The online documentation provides more information about the available methods
for the this object: Orbit.
The next step is to interpolate the orbit ephemerides over time to get the satellite positions for a given relative pass number.
Note
Is it possible to iterate over the relative pass numbers over time periods
using the iterate method.
for cycle_number, pass_number, first_location_date in orbit.iterate(
start_date, end_date):
...
nadir_pass_corrdinates = pyinterp.calculate_pass(2, orbit)
assert nadir_pass_corrdinates is not None
pd.DataFrame({
'time': nadir_pass_corrdinates.time,
'lon_nadir': nadir_pass_corrdinates.lon_nadir,
'lat_nadir': nadir_pass_corrdinates.lat_nadir,
})
print(nadir_pass_corrdinates.equator_coordinates)
EquatorCoordinates(longitude=59.20360095529902, time=np.timedelta64(3087382968771,'ns'))
The variable nadir_pass_corrdinates contains the satellite positions for the given pass: - The nadir longitude in degrees - The nadir latitude in degrees - The time for each position in a numpy.datetime64 array - The along track distance in meters - And the coordinates of the satellite at the equator.
Note
The variable nadir_pass_corrdinates could be None if the pass number
is outside the bounding box defined during the instantiation of the
Orbit object.
See the online documentation for more information about the available methods
for the Pass object.
Finally, we can calculate the satellite positions for a given pass number over a swath.
assert nadir_pass_corrdinates is not None
swath = pyinterp.calculate_swath(nadir_pass_corrdinates)
The swath object contains the properties of the pass, similar to the previous example. Additionally, it includes the coordinates of the satellite over the swath for each location on the nadir track.
pd.DataFrame({
'time': swath.time,
'lon_nadir': swath.lon_nadir,
'lat_nadir': swath.lat_nadir,
})
The DataFrame df shows the longitude and latitude coordinates of the satellite for the first two lines of the swath. The index x_ac represents the across-track distance in meters.
df = pd.DataFrame(
{
'lon_0': swath.lon[0, :],
'lon_1': swath.lon[1, :],
'lat_0': swath.lat[0, :],
'lat_1': swath.lat[1, :],
},
index=swath.x_ac[0, :],
)
df.index.name = 'x_ac'
df
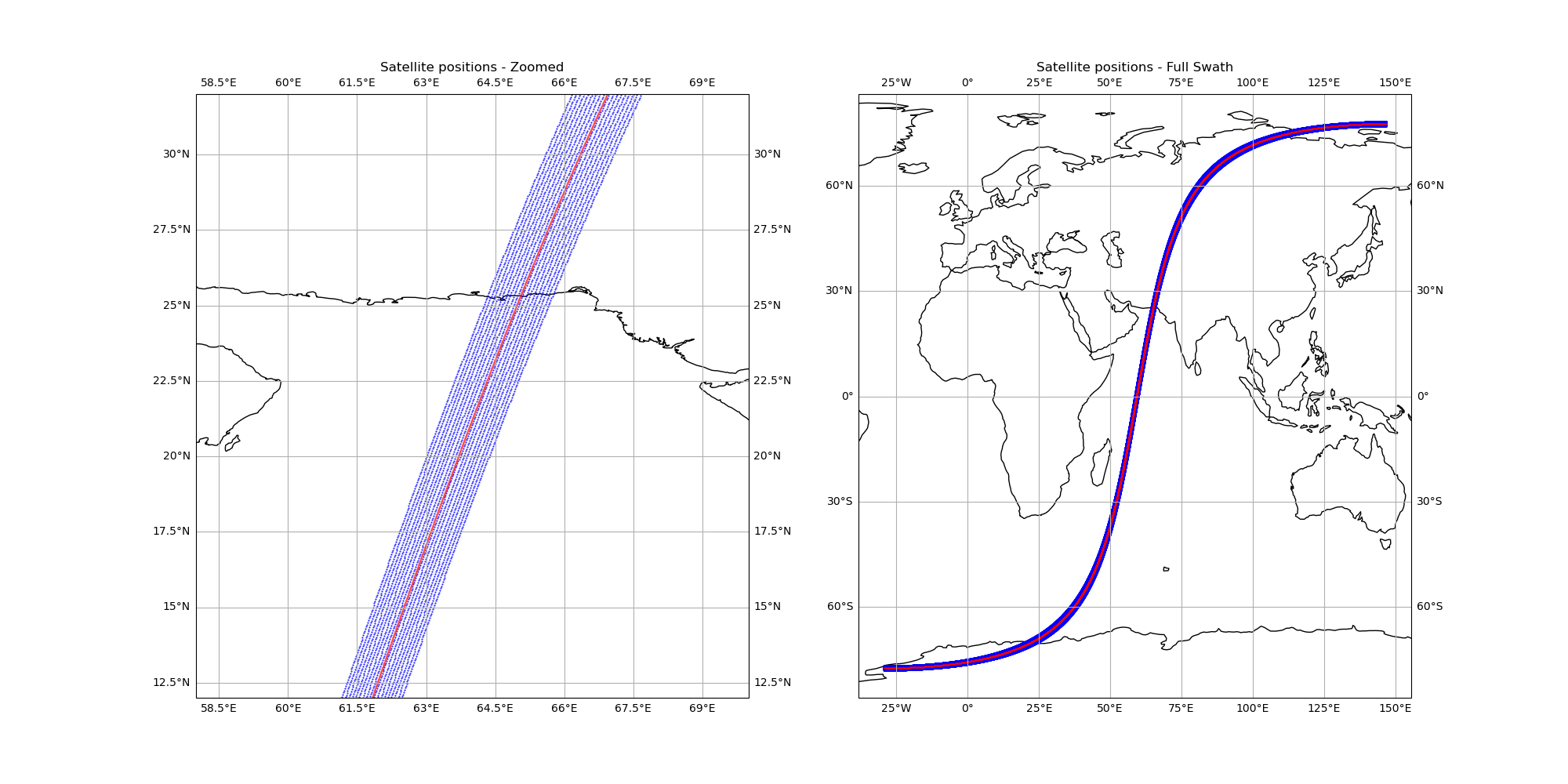
We can plot the satellite positions over the swath using the following code:
fig, (ax1, ax2) = plt.subplots(1,
2,
figsize=(20, 10),
subplot_kw={'projection': ccrs.PlateCarree()})
# Zoomed plot
ax1.set_extent([58, 70, 12, 32], crs=ccrs.PlateCarree())
ax1.plot(swath.lon[::4, ::4].ravel(),
swath.lat[::4, ::4].ravel(),
'b.',
markersize=1)
ax1.plot(swath.lon_nadir, swath.lat_nadir, 'r.', markersize=0.5)
ax1.set_title('Satellite positions - Zoomed')
ax1.coastlines()
ax1.gridlines(draw_labels=True)
# Full swath plot
ax2.plot(swath.lon.ravel(), swath.lat.ravel(), 'b.', markersize=1)
ax2.plot(swath.lon_nadir, swath.lat_nadir, 'r.', markersize=0.5)
ax2.set_title('Satellite positions - Full Swath')
ax2.coastlines()
ax2.gridlines(draw_labels=True)
ax1.set_aspect('auto')
ax2.set_aspect('auto')
plt.show()
Total running time of the script: (0 minutes 0.997 seconds)