Tide mapping example

In this example, we will use the model to predict the tidal elevation on a global grid.

Warning

The model employed is an older FES tidal-atlas model due to its significantly smaller size compared to newer models. Do not use it for real applications. You can download the model from the AVISO website.

First, we import the required modules.

from __future__ import annotations

import os
import pathlib

import cartopy.crs
import matplotlib.pyplot
import numpy
import pyfes

First we create an environment variable to store the path to the model file.

os.environ['DATASET_DIR'] = str(pathlib.Path().absolute().parent / 'tests' /
                                'python' / 'dataset')

Now we need to create the instances of the model used to calculate the ocean tide and the radial tide. To do this, we need to create a YAML file that describes the models and their parameters. The configuration file is fully documented in the documentation.

Note

The content of the configuration file is viewable in the GitHub repository.

handlers: dict[str, pyfes.core.AbstractTidalModelComplex128
               | pyfes.core.AbstractTidalModelComplex64]
handlers = pyfes.load_config(pathlib.Path().absolute() / 'fes_slev.yml')

handlers is a dictionary that contains the handlers to the ocean and radial tide models.

print(handlers)

{'radial': <pyfes.core.tidal_model.CartesianComplex64 object at 0x7fdad9fd5730>, 'tide': <pyfes.core.tidal_model.CartesianComplex64 object at 0x7fdad9fe58b0>}

Hint

By default, the function pyfes.load_config() loads the entire numeric grid into memory. To predict the tide for a specific region, you can use the bbox keyword argument to specify the region’s bounding box. This bounding box is a tuple of four elements: minimum longitude, minimum latitude, maximum longitude, and maximum latitude. Example:

handlers = pyfes.load_config('fes_slev.yaml', bbox=(-10, 40, 10, 60))

We can now create a global grid to calculate the geocentric ocean tide. The grid is defined by its extent and its resolution.

lons = numpy.arange(-180, 180, 1)
lats = numpy.arange(-90, 90, 1)
lons, lats = numpy.meshgrid(lons, lats)
shape = lons.shape
dates = numpy.full(shape, 'now', dtype='datetime64[us]')

We can now calculate the ocean tide and the radial tide.

tide, lp, _ = pyfes.evaluate_tide(handlers['tide'],
                                  dates.ravel(),
                                  lons.ravel(),
                                  lats.ravel(),
                                  num_threads=0)
load, load_lp, _ = pyfes.evaluate_tide(handlers['radial'],
                                       dates.ravel(),
                                       lons.ravel(),
                                       lats.ravel(),
                                       num_threads=0)

We can now calculate the geocentric ocean tide (as seen by a satellite).

geo_tide = tide + lp + load
geo_tide = geo_tide.reshape(lons.shape)

Mask the land values.

geo_tide = numpy.ma.masked_where(numpy.isnan(geo_tide), geo_tide)

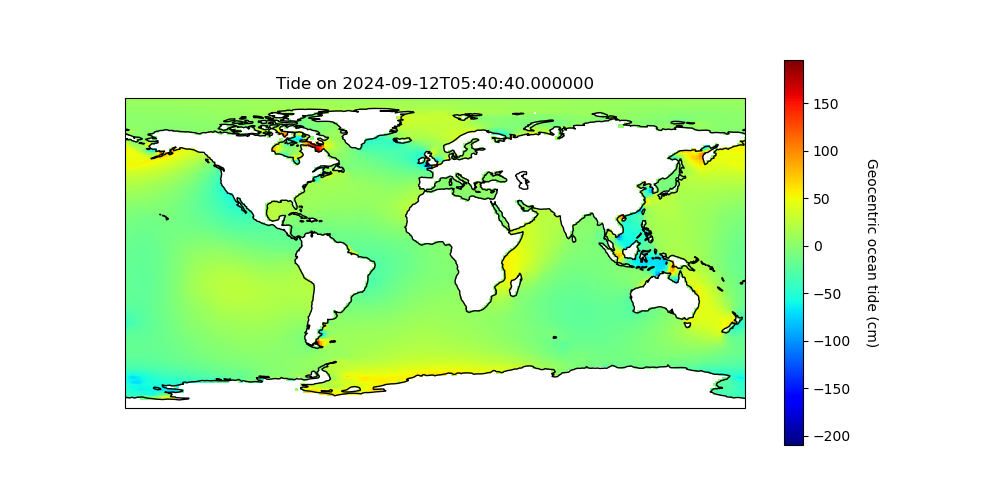
We can now plot the result.

fig = matplotlib.pyplot.figure(figsize=(10, 5))
ax = fig.add_subplot(1, 1, 1, projection=cartopy.crs.PlateCarree())
ax.coastlines()
ax.set_global()
ax.set_title(f'Tide on {dates[0, 0]}')
ax.set_xlabel('Longitude')
ax.set_ylabel('Latitude')
mesh = ax.pcolormesh(lons,
                     lats,
                     geo_tide,
                     cmap='jet',
                     transform=cartopy.crs.PlateCarree())
colorbar = fig.colorbar(mesh, ax=ax)
colorbar.set_label('Geocentric ocean tide (cm)', rotation=270, labelpad=20)