Mesh Interpolation

This example demonstrates how to interpolate a tidal model stored in a mesh using LGP2 discretization.

First, we import the required modules.

from __future__ import annotations

import pathlib

import cartopy.crs
import matplotlib.pyplot
import netCDF4
import numpy
import pyfes

MODEL = str(pathlib.Path().absolute().parent / 'tests' / 'python' / 'dataset' /
            'fes_2014.nc')

Create a function to load one wave from the model.

def load_model(
    model: str,
    wave: str,
    max_distance: float = 0.0,
) -> pyfes.core.tidal_model.LGP2Complex64:
    """"Load a tidal wave model from a netCDF file.

    Args:
        model: Path to the netCDF file.
        wave: Name of the wave to load.
        max_distance: Maximum distance allowed to extrapolate the model if the
            requested point is outside the domain.

    Returns:
        The tidal wave model.
    """
    with netCDF4.Dataset(model, 'r') as ds:  # type: ignore
        lon = ds.variables['lon'][:]
        lat = ds.variables['lat'][:]
        triangle = ds.variables['triangle'][:]
        code = ds.variables['lgp2'][:]

        amp = numpy.ma.filled(ds.variables[f'{wave}_amp'][:], numpy.nan)
        pha = numpy.ma.filled(ds.variables[f'{wave}_phase'][:], numpy.nan)
        pha = numpy.radians(pha)
        values = amp * numpy.cos(pha) + 1j * amp * numpy.sin(pha)

        result = pyfes.core.tidal_model.LGP2Complex64(
            pyfes.core.mesh.Index(lon, lat, triangle),
            codes=code,
            tide_type=pyfes.core.kTide,
            max_distance=max_distance,
        )
        result.add_constituent(wave, values)
        return result

Load the model.

model = load_model(MODEL, 'M2')

Create a grid to interpolate the model. For this example, we use a regular grid over the French coast.

lon, lat = numpy.meshgrid(
    numpy.linspace(-5.0, 10.0, 100),
    numpy.linspace(40.0, 55.0, 100),
)

Interpolate the waves loaded from the model.

values, quality = model.interpolate(lon.ravel(), lat.ravel(), num_threads=1)

Values is dictionary of numpy arrays. Each key is the name of a wave and the value is the interpolated values. Quality is a numpy array of integers. The value is 1 if the point is interpolated and 2 if the point is extrapolated with the nearest point, according to the max_distance parameter.

print(values)

{<Constituent.kM2: 30>: array([       nan+0.j        ,        nan+0.j        ,
              nan+0.j        , ..., 1.49191173+2.69202328j,
       1.41529031+2.70197051j, 1.42119332+2.63657205j])}

Calculate the amplitude of the M2 wave interpolated on the grid.

grid = values[pyfes.core.kM2]
grid = numpy.ma.masked_invalid(grid)
grid = grid.reshape(lon.shape)
grid = numpy.absolute(grid)

Plot the result.

fig = matplotlib.pyplot.figure(figsize=(10, 10))
ax = fig.add_subplot(1, 1, 1, projection=cartopy.crs.PlateCarree())
ax.set_extent([-5.0, 10.0, 40.0, 55.0], crs=cartopy.crs.PlateCarree())
ax.coastlines()
contour = ax.pcolormesh(lon,
                        lat,
                        grid,
                        transform=cartopy.crs.PlateCarree(),
                        cmap='terrain',
                        vmin=0.0,
                        vmax=400.0)
cbar = matplotlib.pyplot.colorbar(contour, ax=ax, orientation='vertical')
cbar.set_label('Amplitude (cm)')
matplotlib.pyplot.show()

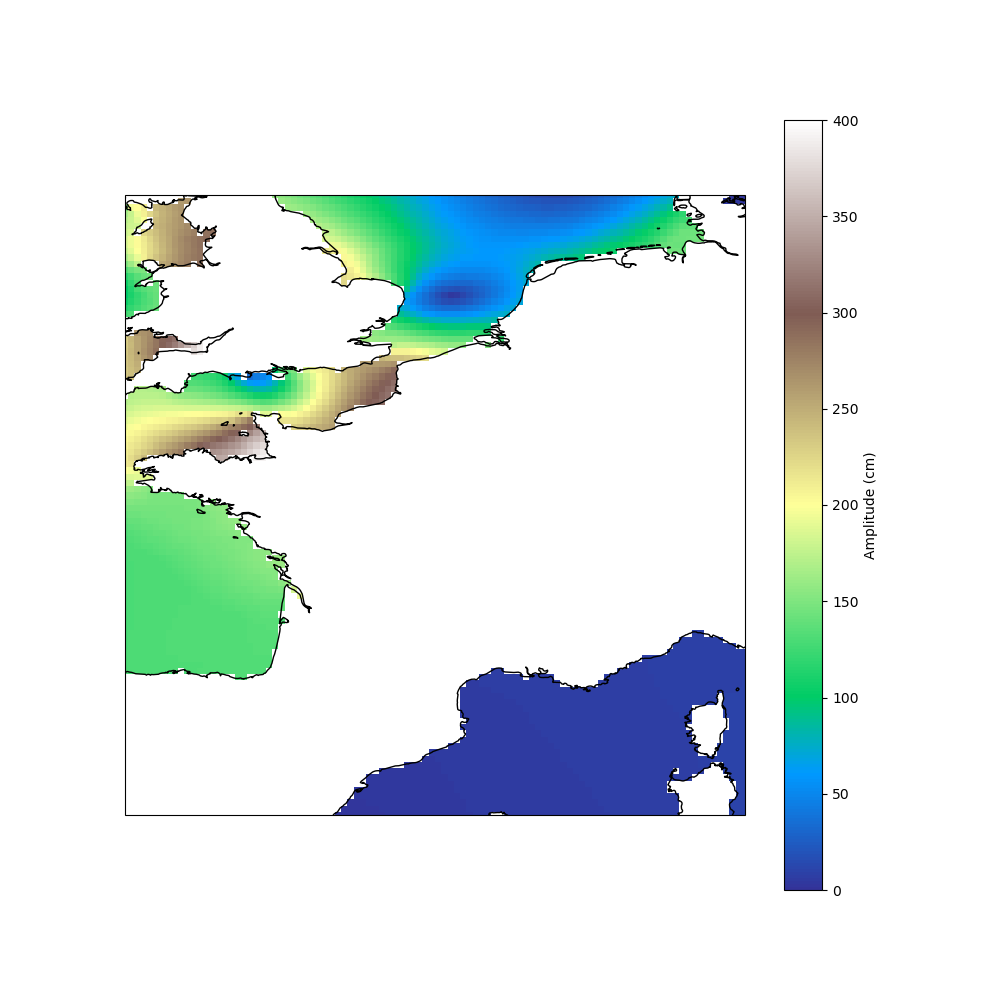
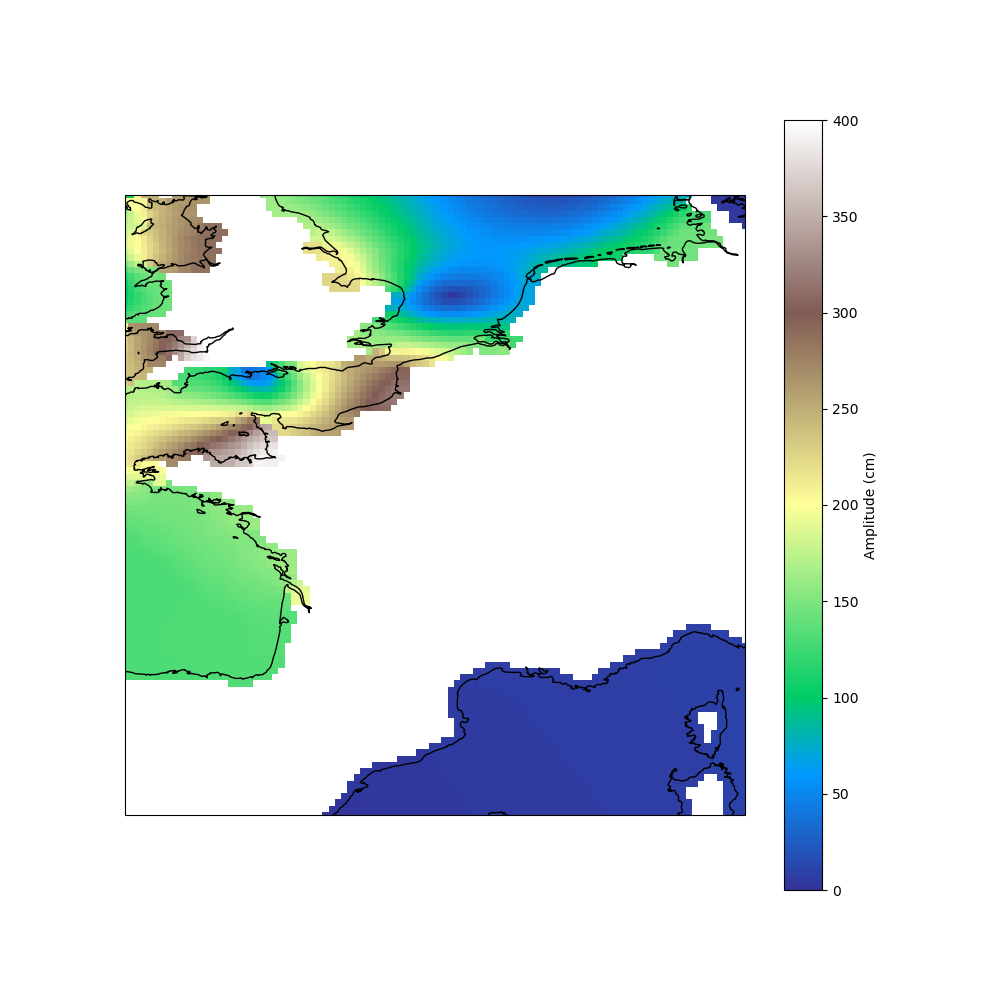
You can observe that the values near the coast are not interpolated. This is because the model is not defined in this area. It’s possible to extrapolate the model by increasing the max_distance parameter. For example, if you set it to 20 km, the model will be extrapolated in the English Channel.

Note

The max_distance parameter is only used for extrapolation. If the point is inside the domain, the model is always interpolated. The distance is calculated on the sphere. The expected unit is meters.

model = load_model(MODEL, 'M2', max_distance=20_000.0)
values, quality = model.interpolate(lon.ravel(), lat.ravel(), num_threads=1)
grid = values[pyfes.core.kM2]
grid = numpy.ma.masked_invalid(grid)
grid = grid.reshape(lon.shape)
grid = numpy.absolute(grid)

Plot the result.

fig = matplotlib.pyplot.figure(figsize=(10, 10))
ax = fig.add_subplot(1, 1, 1, projection=cartopy.crs.PlateCarree())
ax.set_extent([-5.0, 10.0, 40.0, 55.0], crs=cartopy.crs.PlateCarree())
ax.coastlines()
contour = ax.pcolormesh(lon,
                        lat,
                        grid,
                        transform=cartopy.crs.PlateCarree(),
                        cmap='terrain',
                        vmin=0.0,
                        vmax=400.0)
cbar = matplotlib.pyplot.colorbar(contour, ax=ax, orientation='vertical')
cbar.set_label('Amplitude (cm)')
matplotlib.pyplot.show()